您现在的位置是:首页 > 人工智能人工智能
图灵奖得主、《龙书》作者万字长文讲解:什么是「抽象」?
![]() cc博主2022-04-02【人工智能】555人已围观
cc博主2022-04-02【人工智能】555人已围观

编译 | bluemin
编辑丨陈彩娴抽象计算思维以设计问题的抽象模型为中心,应用计算步骤和高效算法解决问题——这一概念不仅服务于计算机科学(CS),而且逐渐渗透到科学和日常生活中。「抽象」(Abstraction)是计算思维的核心,也是本文的主题。「抽象」一直是计算机科学的重要概念,在向广大受众教授计算机知识时,对计算思维的强调更是突显了抽象的重要性。在计算机科学中,抽象并不局限于物理现实,因此我们发现有用的抽象无处不在,例如「量子力学」。它有一种衍生的计算抽象,叫「量子电路」,从物理概念开始,催化出用于模拟的编程语言,以及利用其独特功能的理论算法,有望在大型机器上实现。计算机科学中的「抽象」往往包含以下内容:
- 数据模型包含一种或多种类型的数据以及数据之间可能存在的关系。例如,无向图可以描述为由节点和边组成,每条边连接两个节点。
- 某些编程语言不进行数据操作。这可能是一种传统的编程语言,也可能只进行一些特定的操作。这种语言总是有一个正式的语义——关于程序如何影响数据的规范。
- 一个全集 U。
- 全集 U 的子集 S,初始化时,S为空。
- 插入(x):如果U的元素x不在集合S中,则将其插入集合S中,即 S: = S ∪ {x}。
- 删除(x):从集合S中去除元素x,S:= S – {x}。
- 查找(x):如果元素x在集合S中返回真,否则为假。
- 单元格包含值(某个全集U的成员)和指向另一个单元格的链接(可能为空)。
- 标头,简单命名为指向单元格的链接(可能为空)。
- 全集 U。
- 哈希桶数 B,从 0 到 B-1 编号。
- 从 U 到 {0,1,…,B–1} 的哈希函数 h。每个哈希桶 b 是全集 U 的元素 x 的子集,使得 h(x)=b。
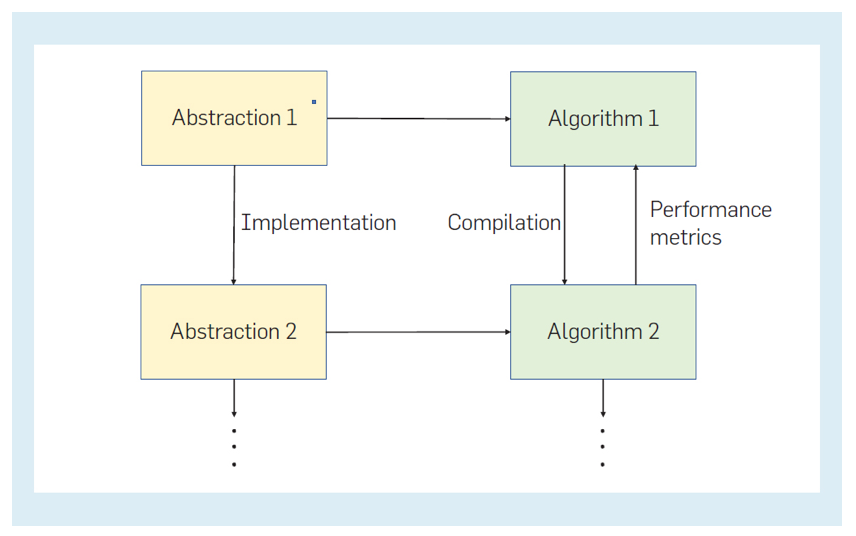
编译器的抽象现代编译器将翻译过程细化为多个阶段,每个阶段将源程序的一种表示形式转换为另一种语义等价的表示形式,通常处于较低的抽象级别。编译器中的阶段通常包括词法分析、句法分析、语义分析、中间代码生成、代码优化和目标代码生成。所有阶段共享的符号表用于收集和提供有关源程序中各种结构的信息。前四个阶段通常称为编译器的前端,后两个阶段称为后端。编译器实现的进展涉及许多重要的抽象。我们将具体讨论三种这样的抽象:正则表达式、上下文无关文法和流图。前两个是带有有趣优化故事的声明性抽象。第三个虽然不是声明性的,但也带来了有趣的实现挑战。2.1 正则表达式和句法分析句法分析是编译器的第一个阶段,它将源程序读取为一个字符序列,并将其映射为一个称为标记的符号序列,然后传递到下一个阶段,即语法分析器。例2.1 如果源程序包含语句:华氏温度=摄氏度*1.8+32,句法分析器可以将该语句映射为七个标记的序列:<id><=><id><*><real><+><int> 。这里id是任何程序变量或标识符的标记,运算符=、*、和+本身就是标记,这两个常量分别被转换为标记real和int。编译器构造方面的一大进步是创建了句法分析的生成器,一个像Lex这样的程序,将标记的描述作为输入,生成一个程序,将源程序分解为标记,并返回与源程序对应的标记序列。使Lex得以应用的抽象是正则表达式。像Lex这样使用正则表达式抽象的系统使用了许多有用的速记,使编写正则表达式更为简单,但不会更改可以在此抽象中定义的字符串集。例2.2 在某些编程语言中,作为合法标识符的字符串集可以定义如下:letter = [a-zA-Z]digit = [0-9]id = letter (letter+digit)* 在这个简写法中,像a-z这样的表达式表示 a 到 z 之间带有ASCII 码的单字符串的并集。因此字母的正则表达式在最初的三个运算符集合中:a+b+...+z+A+B+...+Z类似地定义数字,然后将标记<id>的字符串集定义为字母后跟0个或多个字母和/或数字串组成的字符串。2.1.1 Lex程序产生之前:书目检索从理论研究中可以很好地理解,正则表达式抽象可以编译成几种抽象实现之一,例如确定性或非确定性有限自动机(NFA和DFA)。然而,当需要解决实际问题时,仍有一些技术有待突破。贝尔实验室在首次尝试自动搜索相关文献时采取了一个有趣的步骤:他们在磁带上保存了整个贝尔实验室图书馆的标题,并且开发了软件来获取关键字列表、找到包含这些关键字的文档。然而,当给定一长串关键字时,搜索速度很慢,因为它每搜索一个关键字就会遍历一次磁带。
Aho-Corasick算法对此做了改进,与单独搜索每个关键字不同,关键字列表被视为包含任何关键字出现的所有字符串集的正则表达式,即:
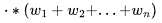
 个状态的DFA,这实际上是不通的。在实践中,最坏的情况发生的概率很小。
个状态的DFA,这实际上是不通的。在实践中,最坏的情况发生的概率很小。然而,在正则表达式的其他应用中,可能并且确实会出现接近最坏情况的情形。grep 是最早的 UNIX 命令之一,代表「获取正则表达式并打印」。该命令将接受一个字符串并确定它是否具有给定正则表达式语言的子字符串。最简单的实现是将正则表达式转换为 NFA,然后再转换为 DFA,让 DFA 读取字符串。当DFA较大时,将NFA转换为DFA比扫描字符串要耗费更多的时间。但是,当正则表达式仅用于一次扫描字符串时,有更有效的方法来实现命令,例如 grep。Ken Thompson 的第一篇研究论文表明,与其将小型 NFA 转换为大型 DFA,不如直接模拟 NFA 更有效。也就是说,读取字符串的 NFA 通常在读取每个字符后处于一组状态中。因此,只需在每个字符之后跟踪这些 NFA 状态,并在读取下一个字符时,从前一组状态构建该字符可到达的状态集。通过 NFA 到 DFA 的惰性转换可以实现更高的效率。也就是说,每次读取一个字符的输入字符串,然后将到目前为止所读取的前缀实际产生的 NFA 状态集制成表格。这些 NFA 状态集对应于 DFA 状态,因此我们只构建处理此特定输入字符串所需的 DFA 转换表部分。如果给定正则表达式的 DFA 不太大,完成处理字符串之前将构建大部分或全部的DFA,会获得直接使用 DFA 的好处,而不是在字符串的每个字符后构造NFA状态集。但是如果DFA比字符串大,大部分的DFA永远不会被构造,所以我们会充分利用这两种情况。这项改进是在名为 egrep 的 grep 版本中实现的。
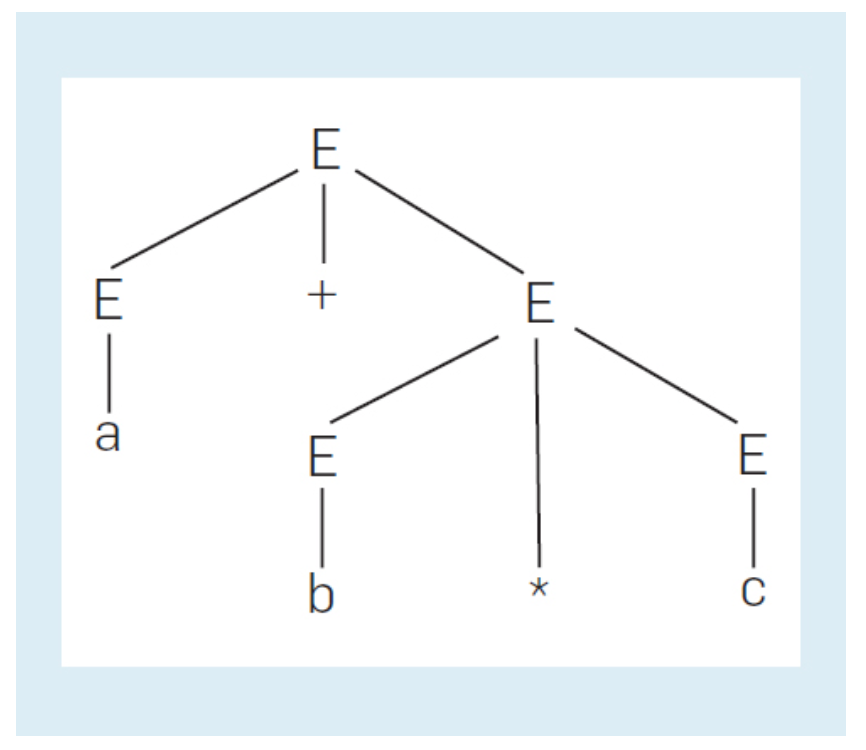
 ,这意味着一种构造表达式的方法是在两个较小的表达式之间放置一个加号。
,这意味着一种构造表达式的方法是在两个较小的表达式之间放置一个加号。2.2.1 LR(k)语法分析 在20世纪60年代,有一系列关于如何从CFG构造高效语法分析器的提议。人们认识到,对于通用编程语言,只要语法具有某些属性,就可以对程序进行一次从左到右的扫描,而无需回溯,并根据该语言的语法构建语法树。有些决定很棘手。例如,在处理表达式a+b*c时,仅读取a+b后,必须决定是否将表达式a和b与加号组合成更大的表达式。如果向前看一个标记并看到*,就会知道把a和b结合起来是不正确的,但必须继续前进,最终把b和c结合起来。只有在此基础上,把a和表达式b*c结合起来才是正确的。这种语法分析方式称为「移位-归约解析」。在扫描输入时,每一步都需决定是通过将下一个输入标记推入堆栈来移动它还是对堆栈顶部的符号进行归约。归约时,归约的符号必须在CFG的右侧。这些符号出栈后被替换到同一产生式的左侧。此外,为产生式左侧的符号创建语法树节点。它的子节点是刚刚出栈的符号对应的树根。如果一个标记出栈,它的树只是一个节点,但如果一个语法类别出栈,那么它的树就是之前为堆栈上的符号构造的树。Don Knuth提出了LR(k)语法分析,适用于最普遍的语法类别,对输入进行单次从左到右扫描,使用移位-归约范式并查看输入前面的最多k个符号后可以正确解析。这项工作似乎解决了语法分析器应该如何构造的问题。然而,并非每个CFG,甚至每个典型编程语言的CFG,都满足成为任何 k 的 LR(k) 文法所必需的条件。虽然普通编程语言似乎确实有LR(1)语法,即仅使用输入上的一个先行符号就可以进行移位-归约分析的语法,但这些语法的设计相当复杂,通常比直观需要的语法类别多出一个数量级。2.2.2 Yacc语法分析的生成器 因此,在 Knuth 的论文之后,有几次尝试寻找使用 LR(1) 解析的方法,但要使其适用于更简单的 CFG。我们受到普林斯顿大学的一位研究生 Al Korenjak 的启发,他的论文是关于压缩 LR(1) 解析器的方法。我们茅塞顿开,对于通用语言,可以从一个非LR(1)的语法开始,仍然为该语法构建一个从左向右的移位-归约解析器。当语法不是LR(1)形式时,在某些情况下,我们也可以使用两种不同的产生式进行归约和移位或只进行归约。但是我们可以通过考虑运算符的优先级并在输入中向前看一个标记来解决实际情况中的歧义。例2.4 考虑例2.3中所提及的情况。在处理输入a+b*c的a+b之后,堆栈的顶部将有E+E,其中a和b之前都被简化为表达式。存在产生式 E → E + E,可以将 E + E 归约成一个 E,并用标签 E 和子式 E、+ 和 E 构建解析树的一个节点。但是 * 优先级高于+, 我们看到 * 作为下一个输入符号,这说明将 * 移到堆栈上是正确的。稍后,我们也移动 c 并将 c 归约为表达式 E。此时堆栈顶部有 E + E * E。我们正确地将前三个符号归约成 E,留下 E + E。现在,将这些符号归约成 E 是正确的,因为没有任何内容输入(或者还有其他不属于表达式部分的输入,例如结束语句的分号)。通过这种方式,我们将生成如图 2 所示的语法树。我们在贝尔实验室的同事 Steve ohnson 采纳了这个想法并实现了一个名为 Yacc的语法分析的生成器。为了帮助解决移位和归约操作之间的歧义,或者两个不同产生式的归约之间的歧义,Yacc 根据产生式出现的顺序进行判断。在两个产生式都可以归约的情况下,无论哪个产生式首先出现都是首选的。为了解决移位和归约之间的冲突,假设在 Yacc 输入文件中首先出现的运算符优先。Yacc很快成为了编译器实现的重要工具,编译器不仅指传统编程语言的编译器,而且包含许多用途更有限的“小众语言”的编译器。与 Lex 一起,Yacc 提供了一种试验新语言句法结构设计的简单方法。这两种工具贯穿学术界整个学期的编译器课程,学生在课程中设计并实现一种新的领域特定编程语言。
大规模数据抽象我们需要几种新的抽象来考虑最大的可用数据集和可用于操作它们的算法。第1.6节的二级存储模型很重要,但也存在其他表示各种形式的并行和分布式计算的抽象。我们将在这里概述最相关的抽象。3.1 数据的关系模型 首先,Codd 的关系模型已被证明是处理大规模数据的核心。简而言之,数据被组织为表或关系的集合,其中两个示例如图 3 所示。左侧是一个名为 Cities 的关系,它有两列:City 和 State。关系的模式是它的名称和列名列表,在本例中为 Cities (City, State)。关系本身是表格中一组行数据或元组。例如,(Toronto, Ontario)是关系 Cities 的其中一行记录。第二种关系称为States,它有名为 State、Country 和 Pop(该州的人口,以百万计)的列。
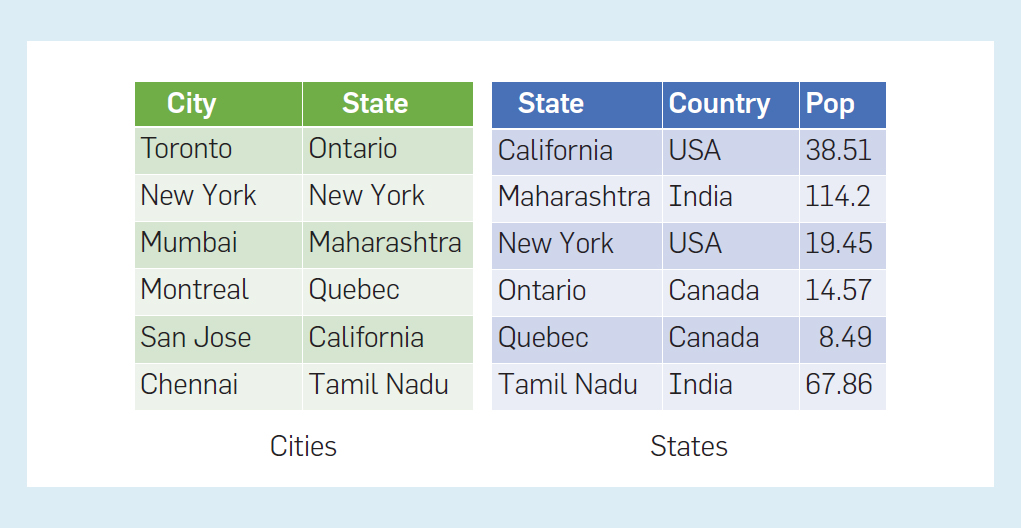
- 选择:在关系R的列名上采用条件C,并返回满足条件C的R行。例如,如果将条件「Country=India」应用于图3中的关系状态,会得到一个新的关系,它的列名为State、Country和Pop,但只包含第二行和第六行状态。
- 投影:为一个关系获取一组列名,并生成一个具有相同行集的新关系,但只包含获取的列。
- 连接:接受两个关系和一个涉及两个关系的列名的条件 C,并通过以下方式生成一个新关系:1)考虑到每一对行,每个关系中的某两行;2)如果这两行中的值满足条件 C,则将两行合并后添加到结果关系中。
 图 4. 按Country分组并对 Pop 求和。随着SQL的发展,更多的功能被纳入标准,包括编写递归程序的能力,以及在通用编程语言中调用代码的能力。因此,原则上,SQL现在是图灵完备的。但绝大多数SQL程序都没有使用使其图灵完备的特性,所以在实践中,仍然有可能以一种利用许多优化机会的方式编译SQL,而这种优化就是我们所说的声明性抽象。3.3 SQL编译 用 SQL 编写的程序通常被编译成低级语言,例如 C语言。C 代码大量使用库函数,例如执行选择或连接等操作。SQL编译的早期阶段(词法分析和句法分析等)与任何通用语言的编译阶段相似。SQL与规范的不同之处在于代码优化阶段(通常称为查询优化)。回想一下,诸如 C 这类语言的优化必须满足在各处保存机器指令,因此将速度提高两倍是一个较好的优化结果。但是SQL和关系模型的操作通常比机器指令强大得多。例如,语法树的一个操作符可以连接两个巨大的关系。因此,与C程序或其同类程序相比,SQL程序由相对较少的步骤组成,但如果按原样实现,这些步骤可能会花费大量时间。因此,SQL 的编译器通常会几乎穷尽搜索等效的语法树,从而减少几个数量级的执行时间。即使花费与SQL程序大小成指数关系的时间来优化一个只执行一次的程序也是有意义的,因为这个程序通常会在较大的关系上执行。3.4 分布式计算抽象 多年来,人们已经认识到单处理器的能力正在达到极限。为了处理越来越大的数据集,有必要开发使用多台独立机器的算法。许多引发我们思考的分布式计算算法的抽象已经实现,并且正在被重点使用。总的来说,这些抽象有一些共同的特点:
图 4. 按Country分组并对 Pop 求和。随着SQL的发展,更多的功能被纳入标准,包括编写递归程序的能力,以及在通用编程语言中调用代码的能力。因此,原则上,SQL现在是图灵完备的。但绝大多数SQL程序都没有使用使其图灵完备的特性,所以在实践中,仍然有可能以一种利用许多优化机会的方式编译SQL,而这种优化就是我们所说的声明性抽象。3.3 SQL编译 用 SQL 编写的程序通常被编译成低级语言,例如 C语言。C 代码大量使用库函数,例如执行选择或连接等操作。SQL编译的早期阶段(词法分析和句法分析等)与任何通用语言的编译阶段相似。SQL与规范的不同之处在于代码优化阶段(通常称为查询优化)。回想一下,诸如 C 这类语言的优化必须满足在各处保存机器指令,因此将速度提高两倍是一个较好的优化结果。但是SQL和关系模型的操作通常比机器指令强大得多。例如,语法树的一个操作符可以连接两个巨大的关系。因此,与C程序或其同类程序相比,SQL程序由相对较少的步骤组成,但如果按原样实现,这些步骤可能会花费大量时间。因此,SQL 的编译器通常会几乎穷尽搜索等效的语法树,从而减少几个数量级的执行时间。即使花费与SQL程序大小成指数关系的时间来优化一个只执行一次的程序也是有意义的,因为这个程序通常会在较大的关系上执行。3.4 分布式计算抽象 多年来,人们已经认识到单处理器的能力正在达到极限。为了处理越来越大的数据集,有必要开发使用多台独立机器的算法。许多引发我们思考的分布式计算算法的抽象已经实现,并且正在被重点使用。总的来说,这些抽象有一些共同的特点:- 它们的数据模型是传统编程语言的模型,但数据分布在许多不同的任务中,我们称之为「计算节点」。实际上,多个任务可能在同一个处理器上执行,但将这些任务视为处理器本身便于分析问题。
- 程序也用常规语言编写,但同一程序可以在各个节点上同时运行。
- 有一种设备可供节点与其他节点通信。这种通信分阶段进行,并与计算阶段交替进行。
量子计算近期,全世界对量子计算和量子编程语言兴致勃勃。量子计算特别有趣,因为量子编程语言中的计算模型与经典编程语言中的计算模型大相径庭。故事从量子力学开始,量子力学是20世纪初期发展起来的物理学基本理论,它描述了原子和亚原子粒子尺度上的自然物理性质。我们将介绍量子力学的基本假设,根据这些假设可以推导出量子力学的所有定律。从这些假设出发,我们可以导出量子电路的抽象,这是量子编程语言的基本计算模型之一。4.1 量子力学的假设复线性代数和希尔伯特空间(具有内积的复向量空间)通常用于描述量子力学的假设。Nielsen和Chuang的著作《量子计算与量子信息:十周年纪念版》是学习这门学科的重要参考书籍。首先,让我们回顾一下在假设中使用的复线性代数的一些基本定义。将运算符视为作用于向量的复数矩阵会对理解很有帮助。矩阵U的厄米特共轭形式为U†,代表矩阵U的共轭转置,即先取U的转置,再对每个值的复数部分求反。酉算子的概念是量子力学的核心。如果UU† = /,则运算符U具有幺正性,其中/ 是恒等式。这意味着每个酉变换的作用都是可逆的。可逆意味着可恢复原状,也就是说,我们可以根据输出重构输入。如果U = U†,则称算子U为厄米特算子,厄米特算子是自伴算子。假设1:孤立物理系统的状态空间可以用希尔伯特空间来建模。系统的状态完全由状态空间中的单位向量描述。假设 1 允许我们将量子比特定义为二维状态空间中的单位向量。量子比特是经典计算中比特(0或1)的量子计算模拟。如果向量
 和
和 用作二维希尔伯特空间的正交基,则该空间中的任意状态向量
用作二维希尔伯特空间的正交基,则该空间中的任意状态向量 可以写成
可以写成 或
或 。其中α和β是复数。因为
。其中α和β是复数。因为 是单位向量,故
是单位向量,故 。
。量子比特
 表现出一种称为叠加态的量子力学的固有现象。与经典计算中的比特总是0或1不同,在α和β未知的情况下,不能说量子比特
表现出一种称为叠加态的量子力学的固有现象。与经典计算中的比特总是0或1不同,在α和β未知的情况下,不能说量子比特 肯定处于状态
肯定处于状态 或肯定处于状态
或肯定处于状态 。我们只能说它是这两种状态的某种组合。
。我们只能说它是这两种状态的某种组合。假设2:封闭量子系统的状态从一个时刻到另一个时刻的演化可以用酉算子来描述。有一种使用薛定谔方程来表述假设2的等效方法。但是,我们在这里只考虑酉公式,因为它自然地引出了量子电路计算模型。假设3:为了从封闭的量子系统中获取信息,我们可以对系统进行测量。以某种概率返回测量结果。可能结果的概率之和为 1。测量会改变量子系统的状态。我们不会深入探讨假设3的细节,但出于讨论的目的,我们可以将单个量子比特
 的测量视为厄米特算子,它以
的测量视为厄米特算子,它以 的概率返回结果0,以
的概率返回结果0,以 的概率返回结果1。回想一下,因为
的概率返回结果1。回想一下,因为 是单位向量,故
是单位向量,故 。测量将状态向量坍缩至二维希尔伯特空间的两个基向量之一。我们注意到,海森堡著名的量子力学不确定性原理可以根据复线性代数规则和假设1-3推导出来。
。测量将状态向量坍缩至二维希尔伯特空间的两个基向量之一。我们注意到,海森堡著名的量子力学不确定性原理可以根据复线性代数规则和假设1-3推导出来。第四个假设展示了当我们组合物理系统时,复合物理系统的状态空间的维数如何增长。假设4:复合物理系统的状态空间是组成物理系统的状态空间的张量积。假设 4 表明,如果我们将单个量子比特添加到物理系统,其状态空间的维度会加倍。因此,如果我们组合n个单量子比特系统,通过取n个单量子比特系统的状态空间的张量积,得到一个状态空间维度是
 的复合系统。状态空间的这种指数式增长使得在经典计算机上模拟大型量子系统的行为将困难重重。
的复合系统。状态空间的这种指数式增长使得在经典计算机上模拟大型量子系统的行为将困难重重。4.2 量子电路从量子力学的四个假设出发,我们可以导出一个称为「量子电路」的计算模型,这是量子编程语言的基本抽象。量子电路由量子门和量子线路组成。它们类似于经典计算中的布尔电路,但有几个重要的区别。将量子门视为复数的正交矩阵,并将其输出视为通过将矩阵应用于输入向量而获得的向量,这对于分析很有帮助。1)单量子比特门单量子比特门有一条通向门的线路和一条引出门的线路。输入线路将一个量子比特
 馈送到量子门。该量子门将酉变换U应用于传入的量子比特
馈送到量子门。该量子门将酉变换U应用于传入的量子比特 ,并将输出的量子比特
,并将输出的量子比特 传送到输出线路上。
传送到输出线路上。在经典的布尔电路中,只有一个非平凡的单位逻辑门,即布尔非门。在量子电路中,二维复希尔伯特空间中的任何酉变换都可以是单量子比特的量子门。这里介绍两个重要的单量子比特门。例 4.1 量子非门,通常表示为X,将量子比特
 映射为量子比特
映射为量子比特 。从根本上说,它翻转了二维希尔伯特空间中表示量子比特的向量系数。注意
。从根本上说,它翻转了二维希尔伯特空间中表示量子比特的向量系数。注意 以及
以及 。
。量子非门X可以用
 矩阵表示:
矩阵表示: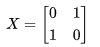
 映射成量子比特:
映射成量子比特: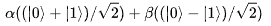
 矩阵表示:
矩阵表示: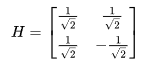
 的复数矩阵表示,该矩阵的行和列是正交的。
的复数矩阵表示,该矩阵的行和列是正交的。例4.3 受控非门(简称CNOT)是一个非常有用的双量子比特门。它有两条输入线和两条输出线,一条称为控制线,另一条称为目标线。开关作用的动作如下:如果控制线的输入量子比特为
 ,则目标线上的量子比特将不变地通过;如果传入的控制量子比特为
,则目标线上的量子比特将不变地通过;如果传入的控制量子比特为 ,则翻转目标量子比特。在这两种情况下,控制线的量子比特都不会发生改变。如果
,则翻转目标量子比特。在这两种情况下,控制线的量子比特都不会发生改变。如果 表示为
表示为 (量子比特
(量子比特 和
和 的张量积),那么我们可以将CNOT 门的作用描述如下::
的张量积),那么我们可以将CNOT 门的作用描述如下::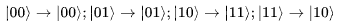
 中引入单个量子比特,并产生一个概率经典比特作为输出,以
中引入单个量子比特,并产生一个概率经典比特作为输出,以 的概率取值为0或以
的概率取值为0或以 的概率取值为1。
的概率取值为1。我们用一个例子来结束量子电路的讨论,这个例子阐释了量子计算的一个不同寻常的特性:纠缠。
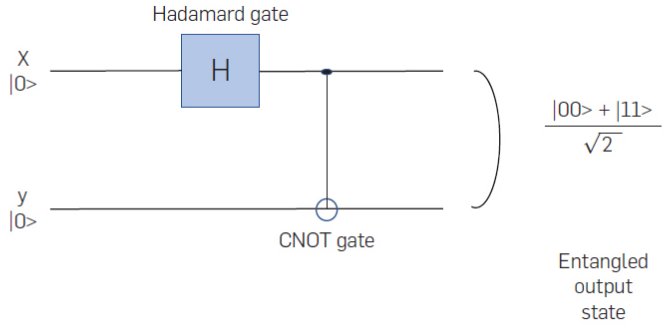
 的四个值的变换:
的四个值的变换:
可以将量子电路的操作描述为状态向量的序列,这些状态向量展示了在应用每一级门之后量子系统的状态。对于图5,将各阶段获得的状态向量总结如下:1)H门之前:

2)在H 门之后CNOT门之前:

3)CNOT门之后:

复合量子系统的状态不能写成其组成系统状态的张量积,这称之为纠缠态。可以看出上面的 EPR 输出状态是纠缠的。不存在两个单量子比特状态
 和
和 使得下式成立。
使得下式成立。
纠缠在量子计算中的作用至关重要,但纠缠的物理现象对物理学家来说仍然是一个谜。事实上,爱因斯坦称其为“超距离的幽灵效应”。4.3 量子算法量子计算设备很可能被用作由经典计算机控制的辅助设备。量子计算机程序通常表示为经典计算和量子算法的混合体。量子算法经常呈现为具有以下结构的量子电路:1) 电路开始时将所有输入量子位设置为特定状态,通常为
 。
。2)电路处于叠加状态。3)电路通过幺正门作用于这种叠加。4)通过测量门将经典比特(0 和 1)作为输出返回到控制的经典计算机,对电路中的量子比特进行测量。量子计算在 1994 年迎来了飞跃式发展,当时贝尔实验室的Peter Shor发表了一种在混合经典计算机/量子计算机上分解n位整数的算法,其时间复杂度为
 。即使今日,也没有可以用多项式时间在经典计算机上分解整数的算法。
。即使今日,也没有可以用多项式时间在经典计算机上分解整数的算法。Shor利用经典数论将整数分解问题简化为寻序问题。求序问题如下:给定正整数x和N,其中x<N 且x互质于N,求最小正整数r,使得
 。整数r被称为N中x的阶数。例如,21中5的阶数是6,因为要使
。整数r被称为N中x的阶数。例如,21中5的阶数是6,因为要使 成立,6是最小的正整数。
成立,6是最小的正整数。Shor设计了一种量子算法,用多项式数量的量子门来解决寻序问题。目前还没有已知的算法可以在多项式时间内解决经典计算机上的寻序问题。量子算法通常使用传统计算机算法中没有的特殊技术。例如,Shor的算法使用量子傅里叶变换作为其寻序计算的一部分。
未来方向抽象对计算机科学的许多领域产生了相当大的影响。关于计算机科学中的抽象故事还有更多的论文。以下是一些理论研究者可能会感兴趣并且具有实际意义的方向。5.1 量子未来量子计算仍然是一个刚刚起步的领域。虽然量子电路可以将任意单一算子近似到任何期望的精度,但今天的量子门计算机只有50到100个可用的量子位。此外,实用的量子算法屈指可数,因此在量子计算的硬件和算法领域都需要做更多的工作来克服这些限制。在理论上,许多悬而未决的问题也仍然存在。例如,如果我们可以证明不能在多项式时间内在经典计算机上分解整数的问题,那么我们将有一个量子计算机比经典计算机更快地解决问题的示例。这只是许多尚未解决的深层理论问题之一。你可能会希望向 Aaronson 咨询量子抽象中的算法挑战列表。目前研究人员已经开发了许多全栈量子计算编程语言。哥伦比亚大学的博士生 Krysta Svore 表明,第 2 节中讨论的编译器架构可以与纠错结合到量子计算设计工具的分层软件架构中。毕业后,她加入了微软研究院,在那里她和她的同事随后开发了 Q# 量子编程语言,它是微软量子开发工具包的一部分。5.2 计算机系统和硬件的抽象 映射归约和其他针对特定类型计算平台(本例中为计算集群)的高级抽象的成功表明,其他平台可能也有类似的抽象。例如,目前人们对无服务器计算很感兴趣,其中数据仅保存在文件系统中,并且通过在短时间内租用一台或多台服务器来完成计算。在较小的规模上,专用硬件是一种增长趋势,并且很可能在加速对大规模数据执行重要算法方面发挥越来越重要的作用。你可能听说过图形处理单元(GPU)和现场可编程门阵列(FPGA)。Plasticine 是设计的另一种用于支持高通信带宽和并行性的芯片,可能很快就会上市。拥有与这些体系结构相匹配的高级抽象将行之有效,因为使用这些抽象编写的算法可以利用一种或多种芯片类型编译成高效的实现。5.3 抽象分类法 多年来,人们发明了与编程语言处理相关的强大抽象,帮助编译器设计领域从一门艺术转变为一门科学。但最后的论文还没有写完。扩展我们在 1.2 节中抽象的基本分类法以涵盖更多编程语言和编译器领域,甚至更多的计算机科学领域,这将大有裨益。与连续运行的系统(如操作系统、网络和互联网)相关的抽象自然会包含在内。此外,我们希望通过数据结构课程中组织的讲座,大家能认识到分类法的强大远不止如此。我们更希望研究是什么让一种抽象比另一种更有用。例如,我们在 3.1 节中提到关系模型如何自然地成为声明性抽象,而以前的数据库模型不适合 SQL 等语言,这为高阶编程的出现奠定了条件。类似地,正则表达式似乎非常适合描述编程语言标记和其他有趣的字符串集,而等价的表示法,例如 Chomsky 的 type-3 语法(CFG 的一种特殊情况)在句法分析等应用程序中从未发现太多用途。可能自然会问:“为什么会这样?”一个有趣的新领域是使用机器学习来创建使用数据而不是用某种编程语言编写的源程序的软件应用程序。从某种意义上说,机器学习是一种不涉及传统编译的软件创建方式。可以指导使用机器学习有效创建强大应用程序的抽象将受益匪浅。
原文链接:
https://cacm.acm.org/magazines/2022/2/258231-abstractions-their-algorithms-and-their-compilers/fulltext

雷峰网(公众号:雷峰网)
雷峰网版权文章,未经授权禁止转载。详情见转载须知。
Tags:电脑免费梯子
相关文章
- 永久免费酸酸乳节点账号及链接分享网站-2022年固定每日更新
- 华为宣布完成监事会换届选举,孟晚舟正式晋升为华为轮值董事长
- 香港云服务器cn2 1核2G 2M 不限流量 26.4元/月 美国云服务器 2核1G 10M不限流量 60元/月 共享ip 2核1G 10M 5.5元/首月 香港高防150G空间 20元/月 学生空间雷电云网络
- 迎战不确定性,企业组织力重要性日益凸显 ——肯耐珂萨独家解读中国企业组织能力调研白皮书
- 香港云服务器1核 1G 3M17.5元/月 美国云服务器1核 1G 10M 17.5元/月XOVV
- 3千亿芯片巨头紫光重组案将进入实质交割,600亿投资款已到位
- 高端市场大获成功,年出货量遥遥领先,中国投影机市场看极米
- 发展SEO优化思维是企业推广一致追求的目标
- 万字深度好文!视觉-语言(VL)智能:任务、表征学习和大型模型
- 服务7亿人,个人客户金融资产超15万亿,建设银行启用企业微信加速数字化战略转型
猜你喜欢
Z-Blog首页显示指定页面的方法
建站
用过WordPress的用户都知道,在WordPress系统里,首页显示有两种方案,一种是显示最新文章,另一种是显示一个静态页面,设置地点在“外观”-“自定义”-“主页设置”里,这个功能对于制作企业或非博客类网站很有用。 而在Z-Blog中,并没...
阅读更多2022永久稳定ssr节点机场,免费的v2ray节点每日更新6.27
技术好文
2022永久稳定ssr节点机场,免费的v2ray节点每日更新,今日周一,为大家提供最新白嫖ssr节点及v2ray节点链接分享账号链接付费节点点击右侧栏目图。资源在2022年6月27日17点更新。免费资源并不容易。请珍惜它。蜗牛SEO将继续更新可用资源,并尽最大...
阅读更多ACL 2022 共收录4篇词义消歧论文,3篇来自一个意大利科研团队
人工智能
作者 | Antonio编辑 | 陈彩娴ACL 2022已经于近期正式在官网上刊登了录取的文章,其中涉及到词义消歧(Word Sense Disambiguation, WSD)的文章共有4篇,参考下图的查询。WSD是指识别出有多个义项的目标词汇在上下文...
阅读更多网站导航如何做SEO优化呢?
站长动态
网站导航如何做SEO优化呢?网站导航在整个网站中起着不可替代的作用,让访客在网站中不会迷失方向,但目前大多数网站的导航都千篇一律,甚至有的为了美观或者单方面的个人需求而放上去,不仅没有节约客户浏览时间,还增加不必要的垃圾页面,那么网站导航如何优化呢?重点要...
阅读更多性功能障碍怎么保健呢
健康问答
性功能障碍已经成了困扰很多人的问题,所以如何治疗性功能障碍,要吃那些食物才能恢复健康已经引起了人们的高度重视,为了患者的健康生活,患者一定要积极的保健调养,那么性功能障碍怎么保健呢,针对这一问题,下面就一起来具体了解一下吧。性功能障碍的患者在平常生活中应该...
阅读更多
















